_/_/_/_/_/
関数は、ハコのことです。
_/_/_/_/_/
***
はじまりました、数学シリーズ。
「重要かつ必要」なところだけ、
つまり「よく使うもの」を丁寧に説明していきますのでご安心ください。
受験勉強するわけじゃないので、細かい知識までは不要ですからね。

本格的に稼げるようになりたいのであれば、
プログラミングの知識だけでなく、数学の知識も積み重ねていかなくてはなりません。
資本主義の世界では、
特殊な技術を持った少数派ほど、稼げますからね。
数学を、コードに落とし込む。
そしてそのプログラムが返す数値を数学的に捉えることで、予測・経営に活かしていく。
それが、エンジニアだったりデータサイエンティストです。
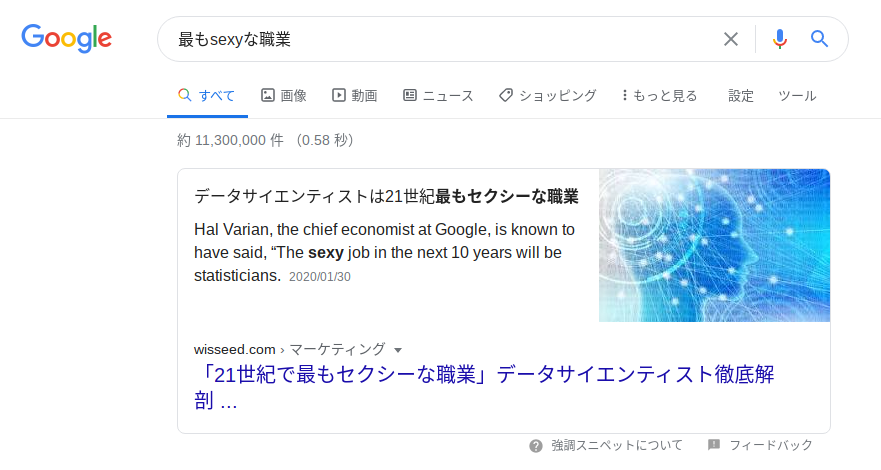
データサイエンティストってご存知ですか?
21世紀、最もSexy
と言われている職業です。
コードを書くだけであれば、AIでもできますからね。
プログラミング×数学×マーケティング
で、市場価値アップ・競争優位に繋げていきましょう。
ということで講義をしてまいります。

さて、
第一回は、プログラミングでもつかう、「関数」という言葉。
これは数学由来の言葉です。
今回は、数学の世界でどう使われていくか見てきましょう。
(プログラミング的使い方は、後日お話しします)
「関数」は英語でfunctionなので、その頭文字fを使って、
f(x)
と表記することが多いです。
読みは「えふえっくす」ですね。
別にfである必要はなく、g(x)と書いてみたり、
例えばPriceについての関数ならP(x)と書くこともあります。
中身もxではなく、f(t)とかf(s)とか書くことだって、あります。
そういう場合は、
数式の前後に、必ずきちんと日本語で何かしら書いてくれているので、
丁寧に読んでみてください。
実はこの「関数」という言葉、昔は「函数」と言ってました。
そうです。
はぁ〜〜〜〜るばる〜、来たぜ、函館ぇ〜!
https://youtu.be/FMIXeHodWEE
のハコです。
なんでハコ?って話なんですけど、
関数には、ブラックボックスのイメージがあるからなんですよね。
ブラックボックスってご存知ですか?
仕組みはよくわからないけど、
どうもあるルールに基づいて、
インプットからアウトプットを返してるっぽい…
そういうのをブラックボックスと言います。
「内部構造がワカラナイもの」を総称してブラックボックスと言います。
(エンジニアの世界には”ブラックボックステスト”というのもありますよね)

私達にとってはパソコンもiPhoneも、ブラックボックスです。
確かに、スイッチを押せば電源がつきます。
が、その仕組み・内部構造はわかりません。
でも、とりあえず押せば点くことはわかります。
こういうのがブラックボックスですね。
数学の世界でブラックボックスとはなにかというと…
たとえば、こんな感じのものです。
あるハコのルール
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄
1→[ハコ]→1
2→[ハコ]→4
3→[ハコ]→9
4→[ハコ]→16
このハコのルール、お分かりいただけますか?
そうです、このハコには、
「入ってきた数字を2乗して出す」
というルールがあります!
この、ハコの仕組みのことを、関数と言います。
このルールのことを、関数と言います。
そしてこのルール、いちいち
●→[ハコ]→▲
って書くのめんどくさいですよね。
っていうかダサいですよね。笑
それをかっこよくしたのがf(x)です。
x→[ハコ]→f(x)
このように、
入れたものをx
出てきたものをf(x)
という風に書きます。
これをつかって、「あるハコ」に入れたもの、出てきたものを
f(x)表記すると、こんな感じになります。
たくさんの例を見れば、慣れてくると思いますんで、たくさん例示します。w
1→[ハコ]→1
は、出てきたものf(1)が1なので
f(1) = 1
2→[ハコ]→4
は、出てきたものf(2)が4なので
f(2) = 4
3→[ハコ]→9
は、出てきたものf(3)が9なので
f(3) = 9
4→[ハコ]→16
は、出てきたものf(4)が16なので
f(4) = 16
と書きます。
このようにして、入れたものと出てきたものの関係を表記します。
例えば、inを入れたら、出てくるのはf(in)です。
さて、ここまで、inputとoutputの関係だけを見てきました。
ブラックボックスの中身は、無視してきました。
次は中身について、解き明かしていきます。(もうすぐ終わります!)
ここまでは、飽くまでも数値を使った具体例でしかありませんでしたが、
もっと、一般的(=すべてを網羅するよう)に表現したらどうなるか?を考えます。
f(1) = 1 × 1 = 1
f(2) = 2 × 2 = 4
f(3) = 3 × 3 = 9
f(4) = 4 × 4 = 16
でした。
このハコに、具体的な数値ではなく、●を入れてみましょう。
f(●) = ●×●
ですよね。
2乗のマークを使うと
f(●) = ●^2
です。(ウェブの世界では2乗をこう書きます)
そして、
●ってダサいから、xを使って書く
ようにすれば、関数の内部構造を表記できます。
f(●) = ●^2
ってダサすぎるから
f(x) = x^2
って書こうや、
ということですね。
●をxに書き換えるだけです。
これが関数f(x)の内部構造の表現です。
逆に、
f(x)にx=3を入れた(代入した)値を算出したければ、
f(x)内の、ありとあらゆるxを3に書き換えれば良いです。
f(x) = x^2
なので…
f(3) = 3^2 = 9
ですね。
他にも
f(5) = 5^2 =25
f(10) = 10^2 = 100
f(0.1) = 0.1^2 = 0.01
という風に算出できます。
大丈夫でしょうか?
では、最後にちょっと練習しときましょう。
【練習1】
f(x) = x + 10
とする。x = 1,5,20としたときのf(x)の値は?
【練習1】の答え
x = 1としたとき
f(1) = 1 + 10 = 11
x = 5としたとき
f(5) = 5 + 10 = 15
x = 20としたとき
f(20) = 20 + 10 = 30
となります。
【練習2(ちょっとムズい)】
次を満たすようなf(x)は?
※f(x)は1次関数とする
f(1) = 1
f(2) = 3
f(3) = 5
f(4) = 7
f(5) = 9
f(6) = 11
f(7) = 13
【練習2の答え】
まず観察します。
数値をインプットすると、
“インプットした数値”番目、の(正の)奇数が返ってきてます。
つまり、「xを入れるとx番目の奇数が返ってくる」わけです。
さて、「奇数」の扱いが問題ですね。
急ですが、奇数の前に、偶数を考えます。
偶数は2で割り切れる数、つまり2の倍数ですね。
だから偶数は、2×●とかけます。
奇数は、どう考えるかというと、
_/_/_/_/_/_/_/_/_/_/
【偶数の1つ隣】
_/_/_/_/_/_/_/_/_/_/
と考えます。
数式では
奇数=偶数+1
か
奇数=偶数ー1
ですね。つまり
2×● +1
か
2×● ー1
ですね。
今回与えられたものをよく観察すると、
f(1) = 1
という条件により、
●=1としたときには、1が帰ってきて欲しいので、
2×●ー1
の法を採用すれば、ぴったり表現できますね。
(2×●+1だと、●=1を入れると3が帰ってきちゃうので、ダメ。)
なので、ダサい●をカッコいいxに書き換えて、
f(x) = 2x – 1
とすれば良いわけです。
練習2はちょっと難しかったですが、練習1のほうは大丈夫でしょうか?
…大丈夫?
おめでとうございます!
これでテキストにf(x)とかg(x)みたいな数式が出てきても、ビビって飛ばす必要がなくなりました!
しかし!
まだまだキモチワルイ記号はたくさんあります!
しっかり勉強していきましょうね!
〜続く〜

