_/_/_/_/_/
シグマは
「下から上までカウントアップして、全部足す」
という意味です。
_/_/_/_/_/
***
本日は、
Σ
について見ていきます。
これ、読み方はご存知じゃないでしょうか?
特に、青春時代をガラケーと共に過ごした方。笑

驚いた顔文字にいましたよね、
Σ(・Д・ノ)ノ
みたいな。笑
今のスマホみたいに、変換では出てこないから
一生懸命「しぐま」で変換してつくったりませんでしたか?
(…え?もしかして、「ぎりしゃ」から行く派ですか?笑)
そうなんです。
Σは「しぐま」と読みます。
意味は
_/_/_/_/_/_/_/_/_/_/
カウントアップしながら全部足す
_/_/_/_/_/_/_/_/_/_/
です。
全部、足します。
でも、じゃあその「全部」って何やねん?
ってことになりますね。
つまり、次の2点が謎なわけです。
- 全部って、どこからどこやねん?
- 全部足すって、何を足すねん?
が謎。
逆に言うと、それらが揃えば、シグマの意味が通るわけですね。
なのでそれを、シグマに書き添えてあげてください。
言葉で表現すると
_/_/_/_/_/_/_/_/_/_/
「何を?」はシグマの右に。
「どこからどこまで?」はシグマの上下に。
_/_/_/_/_/_/_/_/_/_/
図で表現するとこんな風になります。

Σの右にある●。
こいつが「何を足すねん?」の正体です。
この●を、「始」から「終」まで、
1つずつカウントアップしながら、全部足す。
それがこの図・シグマの意味です。
もうちょっと具体的に。
たくさん見まくって、慣れていくほうが良いかもしれません。
たとえば…
小さい頃、お風呂で10まで数えましたよね。
いーち。
にーい。
さーん。
しーい。
って。
「数字を1から10まで全部足す」というのを数学語に翻訳すると、こうなります。
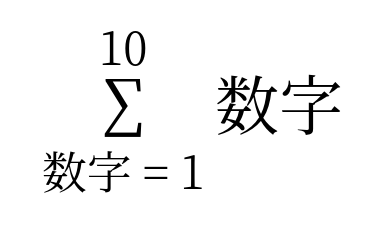
これは、
数字を(1つカウントアップして)2としたものと、
数字を(1つカウントアップして)3としたものと、
…
数字を(1つカウントアップして)10としたものまで、全部足す。
と解釈できるわけです。
そして、「数字」って書くと漢字圏の人達しかわからないので、
number の n に置き換えてワールドワイドにしてあげれば、
こうなるわけです。
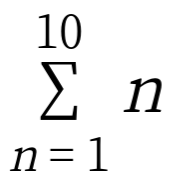
大丈夫でしょうか?
シグマは情報を圧縮してるわけですね。
zip圧縮してます。
だから、
数学に関する本を読んでてシグマが出てきたら、
解凍して意味を理解してあげてくださいね。
こんな風に。
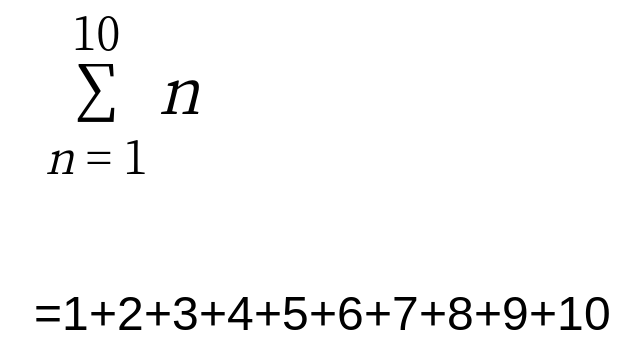
シグマ、だいぶわかってきたんじゃないですか?
ちょっと問題を解いてみましょう。
問題01.
答え01.
さっきと全く同じノリです。
スタート地点が1だったのが、20に変わっただけですね。
なので、こうなります。
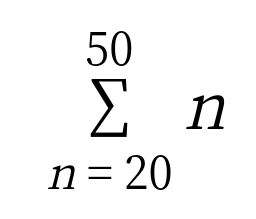
次はちょっとムズカしくしてみます。
問題02.
「正の偶数を小さい方から5個足す」
をΣを用いて表現するとどうなるでしょうか?
わざと日本語も難しくしてみました。
数学後に直訳しづらいですね。
一緒に考えていきましょう。
まずは、シグマの二大情報
- 何がカウントアップされて足されているのか?
- どこからどこまでを考えるのか?
を、日本語で考えてみるのがおすすめです。
あなたがよくご存知の日本語で、まず考えましょう。
アウェイではなくホームで戦うのです。
今回は
1番目の偶数+
2番目の偶数+
3番目の偶数+
4番目の偶数+
5番目の偶数=?
ということですよね。
シグマに必要な2つの情報を考えましょう。
1.何がカウントアップされているか?
「●番目の偶数」がカウントアップしているので、
こいつがシグマの右に来ます。
2.どこからどこまでカウントアップされているか?
シグマの上下に書くスタートとゴールは、
「●番目」のスタートとゴールですね。
今回は1番目から5番目までですよね?
以上の2点を踏まえて、
日本語のままシグマ表記すれば、こうなります。

例によって、●がダサすぎるので、nに書き換えます。

あとは「n番目の偶数」を日本語から数学語に訳してやればよさそうです。
f(x)の回でやったことを思い出してみてください。
偶数ってのは2で割り切れる数のことです。
2で割り切れるということは、2×▲の形をもっているということです。
かっこよく言えば、2の倍数ですね。
偶数を列挙してみましょう。
そう、「にーしーろーはーとー」です。
2、4、6、8、10、12、14、16、…
全部無理やり、2×▲表記にしてみましょう。
1番目の偶数は2=2×1
2番目の偶数は4=2×2
3番目の偶数は6=2×3
4番目の偶数は8=2×4
…
これから
n番目の偶数は2×n
というルールがみえてきましたね。
ということで、求めるシグマ表記はこうなって、ファイナルアンサーです。
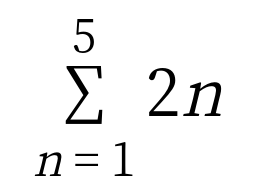
どうですか?
シグマ、わかってきましたか?
よくわからないな〜ということがあれば、
もちろん、ググってみても良いですし、
図書館へ駆け込んでも、
知り合いの理系の人にきいてみてもよいですし、
このまま返信する形で私に質問してもらっても、大丈夫ですよ!(私だけに届きます)
それでは今回はここまで!
〜続く〜
次の講座へ


