_/_/_/_/_/
微分とは、「その瞬間の変化具合」の算出です。
_/_/_/_/_/
もっと簡単にいうと、
微分してわかるのは「その瞬間の勢い」です。
だから、「この勢いで行けば…?」を考えることができて、未来予測ができるのです。
今回はそんな微分の意味がしっかりと理解できるようになっていただきます。
***
数学界のラスボスといえば微積分って感じありますよね。
受験数学界では微分積分について、
「微(かす)かに分かる。分かった積(つも)り。」
という言葉があります。
よくわかんないですけどw
それだけ奥が深いってことですかね?
そんなラスボスに切り込んでいきましょう。

微分って実は、計算自体はむちゃくちゃカンタンなんです。
小学生がやる筆算の方が、手順が多くて難しいくらいです。
ある意味、それができても何もすごくないんです。
逆に、できなくてもいいくらい。笑
それこそ、プログラムにやってもらえば良いんです。
(そんなことできたところでご存知、「コモディティ」ってやつ止まりです。)
だからこそ、大事になってくるのは
「微分って何?」
ってところです。
微分の意味ですね。
定義式をちょっとみてみましょうか。(数学の世界では、定義は丸暗記です。)
関数f(x)を微分するってのは、数学語で言うと、こうです。
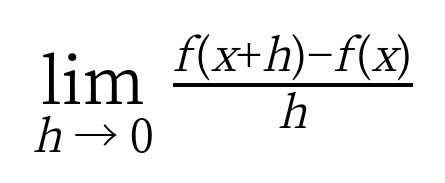
…大丈夫ですか?
見た目の気持ち悪さに、吐き気を催してませんか?w
この画像は何回も出すので早めに慣れてください。笑
某予備校の先生が、
「英語だって言葉なんだ!やれば誰だってできる!」
っておっしゃってます。
数式も言葉なんです。
日本語に変換して、順番に考えていきましょう。
1. 左の謎の英語の意味
2. 分数の分子の意味
3. 分数の分母の意味
4. 分数全体の意味
–復習–
5. 定義式全体の意味
とみていきます。
1.左の謎の英語の意味
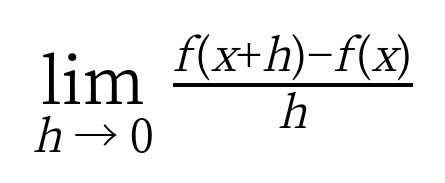
この左側にあるlimってのは、「ギリギリまで近づける」って意味です。
なので、
lim h→0ってのは、「ギリギリまで、hを0に近づける」って意味です。
現時点ではhの正体が不明ですけど、一旦先に進みますね。
2.分数の分子の意味
こんどは右側の分数をみてみましょう。
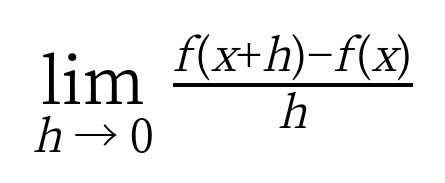
分子はf(x+h)-f(x)で、分母はhです。
分子のf(x+h)-f(x)は何でしょうか?
ここで数学講座シリーズ〜関数編〜が効いてきます。
これは、
「ハコにx+hを突っ込んだ結果」−「ハコにxを突っ込んだ結果」
ですね。
つまり、分母にあるこの引き算が表すのは
_/_/_/_/_/
インプットを +h してみたときの、
アウトプットの変化
_/_/_/_/_/
です。
もっと削ぎ落として表現すると、
ハコに入れるものを変えてみたら、ハコから出てきたものも変わった。
その変化量を表しています。

車の運転で言うと、ハンドルがイメージしやすいですかね?
ハンドルを今より+hだけ傾ける(インプットを変える)と、車の向き(アウトプット)が変わりました。
そのときの、車の向きの変わり具合(アウトプットの変わり具合)です。
それが、分子に来ています。
3. 分数の分母の意味
続いて、分母はhです。
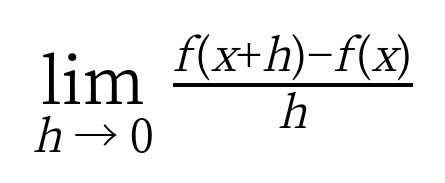
分子は、ハコに突っ込むインプットを変化させました。
その変化量がhでした。
そのhが分母にも、来ています。
つまり、分母のhは、インプットの変化量です。
車で言う、ハンドルの変化量です。
違い、大丈夫でしょうか?
車で言うと、
分母のhは、ハンドルの変化量を表しています。
分子のf(x+h)-f(x)は、車の傾きの変化量をあらわしています。
一般化して数学で表現すると、
分母は、突っ込むものの変化量。
インプットの変化量です。
分子は、(突っ込むものを+hだけ変化させたときの)出てくる結果の変化量。
アウトプットの変化量です。
じゃあ、分数全体が表しているのは…?
4. 分数全体の意味
突っ込むものの変化量に対する、出てきた結果の変化量です。
つまり、
_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/
インプットの変化に対して、
アウトプットがどのくらい変化するか?
_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/_/
です。
まだちょっと、イメージしにくいかもしれません。
ハンドルの例で言うと、この分数は何でしょうか?
(例え話なんで、数値は適当です。)
ハンドルを右に5度傾けた時、車の向きが右に100度変わったとします。
この場合、分母が5、分子が100ですね。
それを計算すると、100÷5=20です。
この数字は、ハンドルの傾き1度あたりの、車の向きの変化です。
なぜか?
ハンドルを+5傾けて、車の向きが+100ということは、
それを5等分(÷5)することで、
ハンドルの傾き+1あたりの車の向きの変化がわかるからです。
つまり、
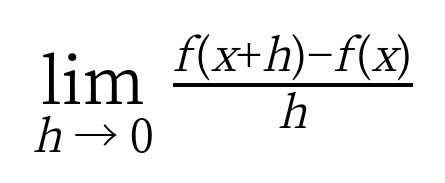
この右半分の分数部分は、
インプットを1変化させた時、
アウトプットはいくつ変化するか?
を表しています。
それをかっこよく言うと「変化の割合」になります。
「割合」って言葉が苦手な方は、「具合」と言い換えてください。
分数全体が表しているのは「変化具合」です。

ハンドルで表現すると、
ハンドルの傾きに対する車の向きの変化具合です。
この値が大きいということは、
ちょっとハンドルを動かすだけで、車の向きがぐうぃ〜んと変わる!ということです。
この値が小さいということは、
ちょっとハンドルを動かしたくらいでは、車の向きはぜ~んぜん変わらへん!ということです。
その車の感度といってもいいでしょう。
さて、
ここまでで前半戦終了なんですけど、どうでしょうか?
ちょっと復習です。
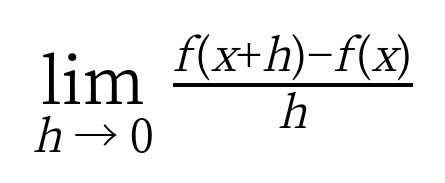
この微分の定義式の、左側の意味と右側の意味がそれぞれわかりました。
左側のlimは、hってやつをギリギリまで0に近づけるという意味でした。
右側は、インプットに対するアウトプットの変化具合。そのシステムの感度です。
大丈夫ですか?
ちょっと休憩しましょう。
ふぅ。
目を閉じて、深呼吸でもしましょう。

ではラスト、いきましょう!(言うて、もう終わりです)
5. 定義式全体の意味
ここからの後半戦では、左側と右側を統合していきます。
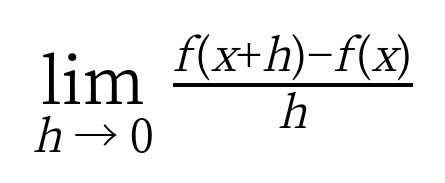
と言ってももう、おわかりかもしれません。
この微分の計算は
インプットを+h(ただしギリギリまで0に近い)に対する、
アウトプットの変化
を計算しています。
車で表現すると、
ハンドルを、ビミョーーーに(ほぼ0)動かしたときの、
車の向きの変化
です。
でも!
よく考えてください。
「インプット量の変化がほぼゼロ」ってどゆこと?
車で考えてみましょうか。
ハンドルの変化がほぼゼロということは、「まさにその瞬間のハンドルの状態」ってことです。
つまり、
ハンドルをほぼ動かしてないその瞬間の、車の向きの変化具合です。
「ハンドルを動かしてない瞬間の変化具合」がイメージしにくい方は、
ハンドルを動かしてないのに、
車の向きが変わってるという恐ろしい状況

をイメージするとわかりやすいです。w
そう、
インプットの変化がほぼゼロってことは、インプットは変わってないわけです。
変わってないってことは、要するに「まさにその瞬間の」って意味になりますね。
だから!!!
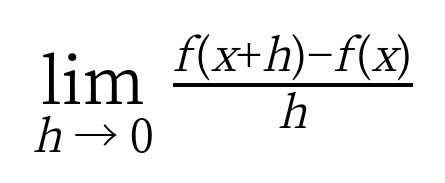
この微分の計算は、
アウトプットの変化具合を算出している
ことになるわけです!!!

どうでしょう?これが、微分です。
もっともっとそぎ落としてシンプルにしちゃえば、
微分とは、変化具合。
ですね。
思い切って表現すれば、
微分とは、「勢い」。
になります。笑
なので
「この勢いで痩せたら、2ヶ月後にはとんでもないことになるぞ!」
というふうに、
勢いから、未来を予測することができるんですね。
ふー!!!繋がりましたね!冒頭のポイントに!
微分とは、「その瞬間の変化具合」の算出です。
_/_/_/_/_/
もっと簡単にいうと、
微分してわかるのは「その瞬間の勢い」です。
だから、「この勢いで行けば…?」を考えることができて、未来予測ができるのです。
今回はそんな微分の意味がしっかりと理解できるようになっていただきます。
ということで、
_/_/_/_/_/
微分とは、「その瞬間の変化具合」の算出です。
_/_/_/_/_/
というお話でした。
いやぁ、お疲れ様でした!
一杯、いっときますか?!
かんぱーい!!!

〜続く〜
次の講座